1.1 UVOD

U svakom tekstu o kalendarima možete naći (ili naići na) pokušaj da se objasni nastanak kalendara. Ne vidim razloga da i ovde ne učinimo slično.

Izgrađujući ono što danas nazivamo civilizacija čovek je u cilju zaštite i pojedinačnih i kolektivnih interesa stvarao sisteme i delove sistema interne komunikacije koji bi mu, ukoliko su dobro zasnovani, mogli pružiti prednost u odnosu na neprijateljsku okolinu. (Termin interno treba shvatiti uslovno: ''do granice mogućnosti kontrole interesa''). Jedan od takvih sistema je bio i sistem za računanje vremena, koji danas prepoznajemo kao KALENDAR. Pri tome, značaj tog sistema se posebno ogledao u obračunu sa neumoljivim neprijateljem čiji su pojavni oblici bili dan i noć, plima i oseka, godišnja doba, sezone kiša, sezone vetrova i sl. Kad na sve to dodamo i pomračenja ''najbližih'' nam nebeskih tela, Sunca i Meseca, jasno je koliko je bilo važno imati mogućnost uspostavljanja tablica redosleda tih događaja. Time se stvarao jedinstven i moćan privid: da redosled događaja kontroliše i njihov nastanak i nestanak.

Koliki je značaj tog privida ilustruje i činjenica da još uvek postoji i koristi se oko 40 različitih kalendara. Srešćete i najveće intelektualce današnjice koji sa beskompromisnom tvrdoglavošću i ubeđenjem koriste vrlo nefunkcionalne, ali ''njihove'' kalendare. Zato, kad u tekstovima o kalendarima sretnete konstataciju da su kalendari u suštini praćeni zahtevima političkih ideala i potrebama veće tačnosti, zapamtite da to ne može biti tačno iznad granica datih (navedenim) pojmom ''interno''. Nijedan pokušaj konvencionalne unifikacije na osnovi dobre volje i naučno-stručnog opravdanja nije u svetu dobio veću podršku i realizaciju od nekoliko desetina procenata svetske populacije.

Ovde ćemo, izuzimajući Julijanski kalendar, dati pregled samo najznačajnijih ''živih'' kalendara. Radi lakšeg praćenja kasnijih izlaganja, ovde dajemo kartu događaja kroz razne kalendarske sisteme i njihovu smenu.

Opšte obeležje svih kalendara je prepoznavanje dana kao jedinice. Time je svaki kalendar postao sistem organizovanja jedinica vremena u svrhu računanja dužih vremenskih intervala. Dakle, konvencija je da je dan najmanja kalendarska jedinica vremena (merenje delova dana se određuje kao održavanje vremena). U kom trenutku ''dan'' počinje bio je problem i rezultat daljih internih konvencija. Kalendari su postali deo veza između čovečanstva i kosmosa. I nije za čuđenje što su kalendari imali oreol svetinje i služili su kao izvor za određenje socijalnog statusa i kulturnog identiteta.

Kalendari su obezbedili osnovu za planiranje životnih i socijalnih ciklusa, za pogađanje i prognozu i za održavanje ciklusa svetovnih i duhovnih događaja. Zajednička je i želja da se jedinice vremena organizuju tako da odgovaraju potrebama i preokupacijama društva.

Bez obzira na opštu jedinicu koristile su se različite metode u stvaranju kalendara. Neki kalendari su replike astronomskih ciklusa po stalnim pravilima, drugi se zasnivaju na apstraktnim neprekidnim ciklusima koji nemaju astronomsko značenje. Neki kalendari se lako izvode iz astronomskih posmatranja, neki su precizno i pažljivo nabrajanje jedinica, a većina sadrži konvencionalne ili nekonvencionalne diskontinuitete i neodređenosti. Mnogi kalendari su provedeni kroz pisane konvencije (u socijlanim sredinama poznato kao zakoni) dok se drugi usmeno prenose i održavaju. Fundamentalne osnove kalendara su jasne ali pažljiva ispitivanja otkrivaju da su čak i standardni kalendari predmet lokalnih uticaja i promena.

Ma kolika da je ''naučna'' savršenost kalendara, oni ostaju deo konvencionalnog stvaralaštva i ne mogu se svrstati u naučna dela. U literaturi je skoro isključivo naglašen istorijski i kulturološki značaj kalendara; ovde ćemo se pretežno baviti njihovom fukcionalnom i konvencionalnom vezom.

Ponavljamo da, uprkos obimnoj literaturi o kalendarima, većina naglašava njihove kulturne sadržaje i značaj ne dajući njihove operativne detalje. Zato nije daleko pomisao da su tvorci i protagonisti kalendara imali različito viđenje njihovog značaja i uloge u društvu.

2.1 ASTRONOMSKE OSNOVE KALENDARA

Kada govorimo o astronomskim osnovama kalendara, govorimo o tome da su pojave, koje su nezavisne i od astronomije i od kalendara, deo predmeta astronomskih istraživaja i izučavanja u nasleđenoj klasifikaciji nauka, ali ne i posledica tog izučavanja. Prihvatajući istorijsko mišljenje o urednoj ponovljivosti i same pojave i njenog trajanja, vidimo da su osnovni astronimski ciklusi dan (zasnovan na trajanju rotacije Zemlje oko sopstvene ose), mesec (zasnovan na trajanju ciklusa u kojem se Mesec nađe u istom položaju u odnosu na Sunce i Zemlju) i godina (zasnovana na trajanju revolucije Zemlje oko Sunca)

Kompleksnost svih kalendara sastoji se u nepostojanosti izabranih ciklusa i u njihovoj međusobnoj nesamerljivosti (nekomenzurabilnosti).

Najnovija astronomska praksa je za odredbu trajanja navedenih ciklusa prihvatila sledeće stavove i izraze.

Tropska godina je definisana kao vremenski razmak između dva uzastopna prolaza Sunca kroz tačku prolećne ravnodnevice na njegovoj prividnoj putanji oko Zemlje. Uzimajući za izabrani period srednju vrednost tih vremenskih razmaka, došli smo do toga da je za dužinu tropske godine usvojena vrednost od 365,2421896698 srednjih ''sunčanih'' dana. Ovaj ciklus je i ciklus godišnjih doba.

Ovde više ne možemo izbeći uvođenje pojma Julijanskog perioda i Julijanskog broja dana. (U daljem tekstu ćemo koristiti samo Julijanski dan). S obzirom na činjenicu da su kalendari zasnovani na cikličnim pojavama, njihovo međusobno povezivanje i upoređenje predstavlja veliku teškoću ako se ne uvede jedna relativno nezavisna, linearna skala vremena, u kojoj će takođe dan biti osnovna jedinica, ali bi se svaki trenutak na toj skali iskazao zbirom proteklih dana od nekog izabranog, početnog trenutka (nul punkta skale, odeljak 14!). Dakle, usvojeno je da je Julijanski dan broj koji daje broj dana proteklih od srednjeg podneva 1. januara 4713. godine pre nove ere julijanskog proleptičkog kalendara. Pri tome, kalendar se naziva proleptičkim kada se njegova primena proširi izvan konvencionalnog intervala (n.pr. identifikacija događaja pre uvođenja kalendara).

Ovde moramo razjasniti još jednu "istoričnu" dilemu: da li postoji "više" prolećnih ekvinokcija (ravnodnevica)? Sa stanovišta građanskog društva, južna i severna zemljina hemisfera su ravnopravne, pa i za stanovnike jedne i za stanovnike druge postoji po ''jedna'' tačka (čitaj: trenutak) prolećnog ekvinokcija. Međutim, sa stanovišta nauke, odnosi su jednoznačno uređeni i kada se govori o tački prolećnog ekvinokcija isključivo se govori o tački preseka sunčeve prividne putanje - ekliptike sa projekcijom ravni nebeskog ekvatora na nebesku sferu, u kojoj Sunce prelazi sa južne na severnu hemisferu. Severna hemisfera je onaj deo nebeske sfere sa koje vidimo da je rotacija Zemlje retrogradna, tj. u smeru suprotnom od smera kretanja kazaljki časovnika.

Mnogi autori u nastojanju ili da izgrade ili da izdvoje pravila za račun Uskrsa (Vaskrsa) mešaju ove pojmove i pogrešno ih navode.

Sinodički mesec je srednji vremenski razmak između uzastopnih konjunkcija Meseca i Sunca i odgovara srednjem ciklusu mesečevih mena. Konjunkcija je raspored u kojem se projekcije Zemlje, Meseca i Sunca na ravan putanje Zemlje oko Sunca, nalaze na jednoj pravoj, u tom redosledu.

Dužina tropske godine i sinodičkog meseca definisane su ovde pod pretpostavkom da dan ima 86400 SI sekundi (sekundi Međunarodnog sistema jedinica).

Iz formula je jasno da se srednje vrednosti trajanja ciklusa menjaju veoma sporo sa vremenom. Isto tako, ''stabilnost'' sinodičkog meseca mnogo je manja od stabilnosti tropske godine.

Prema tome, uspostavljanje samerljivosti nekog od ovih ciklusa sa celim brojem dana, a time i stvaranje kalendara nije lak posao.

Na osnovi pokušaja uspostavljanja što bliže samerljivosti osnovnih ciklusa i jedinice, idvojila su se i tri osnovna modela izgradnje kalendara.

(Zbog veće prirođenosti latinskih korena tih naziva i mi ćemo nazive tih modela zadržati u tom obliku.)

Solarni kalendari, čiji je primer Gregorijanski kalendar projektovan da održava samerljivost sa tropskom godinom. Da bi se to uradilo, umetnuti su dani (formirajući prestupne godine) da povećaju dužinu kalendarske godine.

Lunarni kalendari, kao što je Islamski kalendar, prati ciklus mesečevih mena ne uzimajući u obzir tropsku godinu. Tako su meseci Islamskog kalendara sistematski kraći u odnosu na mesece Gregorijanskog kalendara.

Treći tip kalendara je Lunisolarni kalendar, koji ima skup meseci zasnovan na ciklusu mesečevih mena, ali svakih nekoliko godina se ubacuje još jedan mesec, da bi se kalendar doveo ponovo u fazu sa tropskom godinom. Jevrejski i Kineski kalendar su primeri ovakve vrste kalendara.

3.1 NEASTRONOMSKE OSNOVE KALENDARA: NEDELJA

Kalendari su često sadržali neastronomske osnove, koje su bile ili posledica nekih lokalnih ciklusa ili konvencionalnih intervencija u ređanju dana. U Gregorijanskom kalendaru, nedelja pa i mesec su neastronomske jedinice, mada se mesec može identifikovati i kao astronomski ciklus u drugim kalendarima.

Poreklo nedelje od sedam dana je nepozanto. Prvobitno se ustalila u jevrejskoj tradiciji. Pa ipak, i Biblijski i Talmudski tekstovi pokazuju raznovrsnost konflikta kalendarske prakse. Uostalom, sedam dana na hebrejskom je shabbat, tj. interval posle kojeg dolazi odmor počev od zalaska Sunca u petak do zalaska Sunca u subotu. Sistematski se subota koristila za odmor tek u vreme Vavilonskog egzodusa u šestom veku p.n.e.

Uostalom, broj sedam je imao mistični kosmološki značaj kroz semitske kulture. Upotrebljavao se u vavilonskim i asirskim kalendarima, kao kontinualni ciklus. Mada nedelja od sedam dana može imati poreklo u misticizmu, možda je astronomija dala svoj doprinos tom misticizmu. Sunce, Mesec i planete koje se mogu videti golim okom, čine sedam "lutajućih zvezda". Sedam je i približni broj dana između četiri mesečeve mene, četri puta sedam dana je jedan mesec.

Napomena: postoje i kalendari sa neastronomskom osnovom 8 i 10, ali, kao što rekosmo, nije cilj da ih sve nabrojimo, već da se pozabavimo onim osnovama koje su ''preživele''.

U jevrejskoj praksi, dani u nedelji su bili označeni brojevima, a ne imenima, izuzev što je sedmi dan bio poznat kao Shabbat. Prepoznavanje nedelje i izbor Shabbat-a kao preostalog dana se polako prenelo na Rimljane. Korišćenje imena za oznaku dana u nedelji raširilo se u rimskoj kulturi drugog i prvog stoleća p.n.e. Ova imena su došla iz astronomske prakse imenovanjem svakog dana po planeti koja je ''vladala'' danom. U to vreme Sunce i Mesec su smatrani planetama. "Saturnov dan" se poklapao sa jevrejskom Shabbat. Planetarna imena su polako, mada ne rado, prihvaćena u jevrejskoj i hrišćanskoj kulturi.

Stavljanje nedelje (dan Sunca) u ulogu Shabbat-a (dan Saturna) bio je deo ukupnog otpora Judaizmu. Car Konstantin, koji je doneo znamenti Civilni edikt 321. godine n.e., zabranio je rad prvog dana u nedelji: dan Sunca - nedelja je proglašena prvim danom u sedmodnevnom ciklusu koji je istim ediktom proglašen delom kalendara, a prihvaćen na Nikejskom saboru 325. godine n.e. Pri tome, to je bio dan sećanja na uskrsnuće Isusa Hrista i tog dana nije smelo da se radi.

Prepostavka je da kontinuitet nedelje postoji bez prekida od Biblijskog vremena do danas i da su postupak njegovog očuvanja posebno sprovodile verske institucije. Mada je deset dana izostavljeno iz kalendara u Gregorijanskoj reformi 1582., ciklus dana u nedelji nije poremećen, Tako je 1582. posle četvrtka 4. oktobara Julijanskog kalendara došao petak 15. oktobar Gregorijanskog kalendara.

4.1 REFORME I TAČNOST KALENDARA

Reforma kalendara je izuzetan događaj i u suštini predstavlja pravi društveni potres. Usvajanje kalendara zavisilo je od snaga koje ga uvode i od želje društva da ga prihvati. Na primer, prihvatanje Gregorijanskog kalendara trajalo je preko tri stoleća i na svetovnom nivou taj proces je dobrim delom okončan. Na duhovnom planu, situacija je mnogo složenija.

Usvajanje ovog kalendara u Engleskoj je bilo praćeno sa puno konfuzija, polemika, pa čak i nasilja. To je bio i jak kulturni udar zbog uništavanja tradicionalnih festivala i drugih kalendarskih događaja.

Ipak, pošto su kalendari stvoreni iz društvenih potreba, pitanje tačnosti kalendara je postavljano ako neka od potreba društva nije mogla da se udobno i kvalitetno ostvari zbog grešaka u kalendaru. U takvim situacijama se pribegavalo reformama.

5.1 ISTORIJSKE ERE I HRONOLOGIJA

Izuzev Kineskog kalendara, svi kalendari koje ćemo ovde prikazati broje godine od početnih epoha. U slučaju Kineskog kalendara i nekih kalendara koji nisu ovde opisani, godine se računaju u ciklusima i nijedan ciklus nije izdvojen kao prvi (poseban) ciklus. Neke kulture izbegavaju striktno brojanje godina već svakoj godini dodeljuju ime po nekom događaju koji je obeležio tu godinu. Pa ipak, brojanje godina od izabrane početne epohe je najuspešniji način održavanja dosledne hronologije. Bez obzira da li je ta epoha vezana za istorijska ili legendarna zbivanja ona mora biti povezana sa nekim nizom zabeleženih (istorijskih!?) događaja.

Jedna od ilustracija takve prakse je usvajanje datuma Hristovog rođenja za početnu epohe Hrišćanskog kalendara. Ova epoha je ustanovljena od strane Dionysius Exiguus-a, koji je sređivao tablice Uskrsa. Tabela iz tog vremena pokriva devetnaestogodišnji period (Metonov ciklus) omeđen godinama 228-247, gde su se godine računale od početka vladavine rimskog imperatora Diocletiana. Dionysius je u nastavku te tabele dao tabelu sledeći period od devetnaest godina i označio ga Anni Domini Nostri Christi 532-550. Tako Dionysius-ova Anno Domini 532 je ekvivalentna Anno Diocletiani 248. Na ovaj način je ustanovljena veza između Nove hrišćanske ere i jednog postojećeg sistema (Dioklecijanova era) u kojem je već bilo dosta istorijskih zapisa. Ono što Dionysius nije uradio je da ustanovi tačan datum Hristovog rođenja. Mada istoričari uglavnom veruju da se Hristos rodio nekoliko godina pre 1. godine n.e., istorijski dokazi su suviše neodređeni da bi se odredio definitivan datum. Ovde ćemo, radi kompletnosti pristupa, dati jedno od najpotpunijih objašnjenja šta sve nije tačno, a šta je možda tačno u određenju datuma Hristovog rođenja.(vidi Prilog I)

Jasno je da uvođeje početne epohe (trenutka) nameće problem brojanja i zapisa kalendarskih trenutaka pre početne epohe. Bez obzira na dobru nameru tvoraca svih promena, ta teškoća je dovela do prilične šarolikosti u pristupu, posebno jer u brojevnim sistemima tog doba nula nije imala ni stalnu ni jedinstvenu ulogu, a mnogi nisu ni znali za njeno ''postojanje''. Stoga su istoričari i učevnjaci toga doba uveli praksu da računaju godine unatrag od 1 god. n.e. tako da je 1. godini n.e prethodila 1. godina p.n.e., bez međugodine 0.

Zbog numeričkog diskontinuiteta, ovaj "istorijski" sistem je nezgrapan za poređenje starih i modernih datuma. Danas astronomi koriste +1 da označe 1. godinu n.e. Tada, godini +1 prethodi naravno godina 0, kojoj prethodi godina -1. Pošto se upotreba negativnih brojeva u Evropi polako razvijala, ovaj "astronomski" sistem datuma pojavio se tek u osamnaestom stoleću, kada ga je uveo astronom Jackues Cassini (Cassini, 1740.).

Iako je korišćenje Dionysius-ove Hrišćanske epohe bilo uobičajeno u eklektizmu Srednjeg veka, tradicionalno brojanje godina prema godinama vladavine kraljeva nastavilo je da živi. U šesnaestom veku, Joseph Justus Scaliger pokušao je da reši krpež istorijskih era postavljajući sve u jedan sistem (Scaliger, 1583).

Umesto uvođenja negativnog brojanja godina, on je tražio neku početnu epohu pre istorijskih zapisa. Njegov numerički pristup koristio je tri kalendarska ciklusa: sunčev ciklus, ciklus zlatnih brojeva i indikcioni ciklus. Sunčev ciklus je period posle koga se dani nedelje i kalendarski datumi ponavljaju u Julijanskom kalendaru. Ciklus zlatnih brojeva je period posle koga se ponavlja (približno) mesečeva mena u istim kalendarskim datumima. Indikcioni ciklus je bio rimski poreski ciklus. Scaliger je, prema tome, mogao da okarakteriše godinu kombinacijom brojeva (S, G, I), gde S ide od 1 do 28, G od 1 do 19, a I od 1 do 15. Scalinger je zapazio da će se data kombinacija ponoviti kroz 7980 (= 28 × 19 × 15) godina. Taj interval on je nazvao Julijanski period, pošto je bio zasnovan na Julijanskoj kalendarskoj godini. Za početnu epohu Scalinger je izabrao godinu u kojoj su S, G i I svi bili jednaki 1. On je znao da je 1. godina p.n.e. okarakterisana brojem 9 sunčevog ciklusa, zlatnim brojem 1, a brojem tri indikcionog ciklusa, tj., (9, 1, 3). Našao je da se kombinacija (1, 1, 1) pojavila 4713 godine p.n.e. ili, kako astronomi danas kažu, -4712. Ovo je 1. godina Scaligerovog Julijanskog perioda. Kasnije je to usvojeno kao početna epoha za redni broj Julijanskih dana (videti ranije).

6.1 JULIJANSKI KALENDAR - STARI STIL ^*

Za mnoge savremene svetske institucije treba da zahvalimo starom Rimu, dok stari Rim deo svog institucionalnog stvaralaštva može da zahvali svojim predecesorima: Grčkoj, Egiptu, Vavilonu. Jedna od institucija nasleđenih od starog Rima je i solarni kalendar.

Izvorno, Rimljani su brojali godine od ''osnivanja grada'' (Rima), ab urbe condita, A.U.C. Ako taj trenutak pretočimo u tekući gregorijanski kalendar, to je 753. godina pre nove ere. Godina se sastojala od 304 dana svrstanih u 10 meseci od 30 i 31 dan; godina je počinjala u martu. Rimski vladar Numa Pompilius? je oko sto godina kasnije modifikovao ovaj kalendar napravivši godinu od 355 dana grupisanih u 12 meseci koji su naizmenično imali 30 i 29 dana plus jedan dan viška. Ovaj kalendar je zahtevao dodatni ''mesec'' ( Mercedinus) od 22 ili 23 dana svake druge godine, pri tome posle desetog meseca, decembra, uveden je jedanaesti mesec, Februar pa dvanaesti mesec, Januar.

U toku osvajanja Egipta, 48. godine p.n.e. Cezar je konsultovao Aleksandrijskog astronoma Sosigenes-a o promeni kalendara A.U.C. zbog njegove neadekvatnosti potrebama imperije. Kalendar koji je Cezar usvojio 46. g.p.n.e. bio je identičan kalendaru aleksandrijca Aristarchus-a iz 239. g.p.n.e. u kojem je godina imala 12 meseci tj. 365 dana, a svaka četvrta godina je imala 366 dana. Ne zna se kako je Aristarchus došao do ovog kalendara, ali pretpostavka je da je taj kalendar nastao u Vavilonu.

Sosigenes je predložio da godina 46. p.n.e. ima dve interkalacije (dodatka); prvi ili tekući dodatak od 23 dana, i drugi dodatak koji je trebao da dovede kalendar u sklad sa trenutkom prolećne ravnodnevice, tj. da se ona desi oko 25. marta. Tako je 46. g.p.n.e. imala oko 445 dana i nazivaa se godinom ''zbrke'' (konfuzije). Cezar je želeo da godina počne sa prolećnom ravnodnevicom ili sa zimskim solsticijem, ali zbog tradicije da se Senat sastaje svakog 1. januara, Cezar je na zahtev Senata napravio politički kompromis i prihvatio 1. januar za početak kalendarske godine. (Još 452. g.p.n.e. januar i februar su zamenili mesta).

Na žalost, rimski ''čuvari'' vremena nisu razumeli instrukcije za uvođeje prestupnih godina, pa su ih, umesto svake 4, uvodili na svake 3 godine. Nakupljenu grešku je eliminisao, po svemu sudeći, imperator Avgust, ukidanjem prestupnih godina u intervalu od 10. g.p.n.e. do 4. g.n.e. Prema tome, diskutabilno je koje su godine od 43. p.n.e. do 4. n.e. prestupne; poslednje analize pokazuju da je svaka treća godina počev od 43. p.n.e. do 10. p.n.e. bila prestupna, dakle 43., 40., 37., ... 10. Tada je Avgust ''suspendovao'' prestupne godine i ponovo ih uveo počev sa 4. g.n.e.

Konačno, u vreme Julija Cezara i Avgusta Cezara, dva meseca Quintilis i Sextilis su promenila ime u juli i avgust i, naravno, dobila maksimalnu dužinu od 31 dan. Tako se pojavio mesec Februar sa brojem od 28 dana običnih godina i 29 dana prestupnih godina (ali još se nije pojavio i 29. februar!?).

Julijanski kalendar se i danas koristi u istočno-hrišćanskoj crkvi kao osnovni kalendar za ređanje verskih praznika i događaja.

Dvadesetih godina XX stoleća, na zahtev Srpske pravoslavne crkve poznati srpski naučnik Milutin Milanković uradio je reformu Julijanskog kalendara koja je dovela do njegove samerljivosti sa prirodnim fenomenima na intervalu od 10000 godina, što je bolja samerljivost od Gregorijanskog kalendara za oko 2.2 puta.

Tom reformom se postiglo da se Gregorijanski i Novi julijanski kalendar poklapaju do 4099. godie, a od tada bi Novi kalendar bio tačniji od Gregorijanskog (pojavila bi se razlika od 1 dana). Kako se moglo i očekivati, predstavnici Istočne crkve nisu bili jedinstveni u prihvatanju ove reforme, a posebno je interesantno da i Srpska pravoslavna crkva ni do danas NIJE PRIHVATILA SVOJ PREDLOG!

Zbog posebnog značaja za našu istoriju, ovde dajemo kratak presek Milankovićeve reforme.

6.2 REFORMA JULIJANSKOG KALENDARA

Do početka XX stoleća u zemljama pravoslavne vere (ortodoksno hrišćanstvo, istočno-hrišćanska crkva i sl.) koristio se Julijanski kalendar. Razlika u odnosu na prirodne pojave i Gregorijanski kalendar, narasla je na 13 dana.

Dok je većina država prihvatila Gregorijanski kalendar za zvanični kalendar, njihove crkve su ostale uporne u korišćenju starog stila. Razlozi za neprihvatanje novog stila od strane crkve bili su mahom političke prirode. U heterogenim sredinama poput Kraljevine SHS 1918/1919. godine prihvaćen je Gregorijanski kalendar za oficijelni, državni kalendar, a narod je, u zavisnosti od vere slavio iste verske praznike u raznim trenucima u godini.

Osećajući opasnost od dalje destrukcije Istočne crkve, koja ni do tada nikad nije bila jedinstvena, carigradski patrijarh Meletije je 1923 sazvao Vaseljenski sabor (svepravoslavni kongres) sa jednom tačkom dnevnog reda: reforma Julijanskog kalendara. Svaku delegaciju trebalo je da predstavljaju crkveni velikodostojnici i svetovni naučnici. Delegaciju Srpske pravoslavne crkve činili su mitropolit crnogorsko-primorski, Gavrilo (Dožić) i akademik Milutin Milanković, profesor Univerziteta u Beogradu.

Kako piše Milankvoić u svom izveštaju Akademiji nauka, on se ozbiljno pozabavio stručnim (astronomskim) delom problema, dajući veliku težinu radovima gimnazijskog profesora Trpokivića, koji je, na zahtev SPC (Srpske Pravoslaven Crkve) već bio predložio izvesnu reformu. Usvajajući ono što je bilo dobro i odbacujući neke sporne i nekompletne delove Trpokvićevog predloga, Milanković je za Vaseljenski sabor spremio, u ime SPC, sledeći predlog reforme:

• da se ''preskoči'' 13 dana i novi kalendar sinhronizuje sa Gregorijanskim, jer je on bio tačan u tom trenutku;
• utvrđuje se novo pravilo o interkalaciji (umetanju) dana i dobijanju prestupnih godina tako da: prestupne su one godine koje su deljive sa 4 bez ostatka, s tim što kod sekularnih godina (godina koje označavaju stoleća)
• prestupne će biti samo one kod kojih broj stoleća podeljen sa 9 daje ostatak ili 2 ili 6
• čime se postiže da su i Gregorijanski i Novi Julijanski kalendar tačni do 4100. godine, a posle toga bi Gregorijanski imao grešku od jednog dana
• ovim bi se u novom kalendaru greška od jednog dana akumulirala posle 10000 godina (izvorno: 40000 godina, ali to nije tačno, pr. autora)
• i konačno, predložiti Društvu (Ligi) naroda da usvoji i protežira ovaj kalendar na nivou cele svetske zajednice

Time su sve delegacije dovedene u poziciju da 21. maja 1923. godine glasaju i prihvate predlog carigradskog patrijarha, čemu se usprotivio mitropolit Gavrilo i zatražio da se posebno razmatra predlog SPC, koji će na plenumu delegacija obrazložiti Milanković. To je prihvaćeno i profesor Milanković je 23. maja izneo i obrazložio predlog SPC (vidi gore) koji je, konačno, bio i usvojen 30. maja 1923.

Ratifikaciju ovog rešenja trebale su da izvrše sve autokefalne crkve; Sinod carigradske crkve je to učinio odmah, Grci, Rumuni i Bugari znatno kasnije, a SPC ni do danas.

Napomena: Iz priloženog teksta očigledno je da su verske zajednice, posebno hrišćanska, izabrale metod tablica za određivanje praznika, što je imalo dosta negativnih posledica, posebno kada su u pitanju tzv. pokretni praznici. Pri tome, suština je bila u prihvatanju ciklusa samerljivosti meseca i godine koji je uveo Atinjanin Meton 433. g.p.n.e. Iz tog ciklusa proistekao je tzv. račun epakti, tj. tablični račun mesečevih mena iz kojih bi se odredio datum Uskrsa (Vaskrsa). Kako takav račun nije uzimao u obzir stvarna kretanja nebeskih tela, a time i stvarne trenutke mesečevih mena, što je dovodilo do razlika, Milanković je predložio da se, ubuduće, koriste rezultati astronomske teorije i prakse za određivanje trenutaka pokretnih praznika. Mada je taj predlog usvojen, on nikad nije i primenjen i zato i danas imamo ''celo zamešateljstvo'' u računu tih praznika.

Zbog posebnog kulturnog i istorijskog značaja računa Vaskrsa i samog Vaskrsa ovde dajemo jedan algoritam za račun Vaskrsa, koji je u skladu sa pravilima za račun Vaskrsa za pravoslavne vernike; algoritam je izvorno napravio slavni nemački matematičar Gaus.

Primer: GODINA = 2003; tada je N1 = 8; N2 = 3; N3 = 1; NA = 168; N4 = 18; NB = 118; N5 = 6 pa je
RAZMAK = 18 + 6 = 24
Znači, ako ''potrošimo'' 10 dana za ''popunu'' do 31.03., ostaje nam 14, tj. pravoslavni Uskrs je 14. aprila 2003. po Julijanskom kalendaru ili, ako dodamo 13 dana zaostatka za Gregorijanskim kalendarom, to je 27. april 2003.

6.3 JULIJANSKI DAN I JULIJANSKI DATUM

Sistem Julijanskih rednih brojeva dana je kontinualno brojanje dana koji su protekli od početka Julijanskog perioda, kako je to u šesnaestom veku definisao hronolog J.J. Scaliger (videti raniji odeljak). Mada je Scaligerova prvobitna ideja bila da uvede brojanje godina, astronomi devetnaestog veka su adaptirali sistem tako da se broje dani. John Herschel, 1849. je iscrpno objasnio sistem i dao tabelu: "Razmaci u danima između početka Julijanskog perioda i nekih drugih značajnih hronoloških i astronomskih era".

Julijanski dan 0 je počinjao u Greenwich-ko podne 1. januara -4712., Julijanskog proleptičkog kalendara. Julijanski redni broj dana, izražen kao ceo broj, označava broj celih dana koji su protekli od početne epohe. Julijanski datum (JD) određuje poseban momenat dana završavajući Julijanski redni broj dana decimalom. Na primer, Julijanski redni broj dana 25. juna 1990. je 2448068, dok je Julijanski datum u podne 2448068.0. Ponoć kojom počinje građanski dan je određena oduzimanjem 0.5 od Julijanskog datuma u podne.

Broj dana (1-365) od početka godine je ponekad korisna alatka za čuvanje zapisa. Slabost ove prakse je, kao što smo već jednom rekli, da počne mešanje Julijanskog kalendara sa Julijanskim (redni broj) danom.

6.3.1 JULIJANSKI KALENDAR

Julijanski kalendar, koji je uveo Julije Cezar -45., bio je solarni kalendar sa mesecima fiksne dužine. Svake četvrte godine jedan umetnuti dan se dodavao da se održi sinhronizacija kalendarske godine sa tropskom godinom. Služio je kao standard sve do Gregorijanske reforme +1582.

Danas principe Julijanskog kalendara koriste hronolozi. Julijanski proleptički kalendar je napravljen primenom pravila Julijanskog kalendara na period pre Cezarove reforme. Predstavlja jednostavan hronološki sistem koji povezuje druge kalendare i služi kao osnova za Julijanski redni broj dana.

6.3.2 Pravila

Godine su određene kao normalne godine od 365 dana a prestupna godine od 366 dana Prestupne godine se javljaju u godinama koje su deljive sa 4. U ovu svrhu, godina 0 n.e., (vidi odeljak 7.1) se smatra deljivom sa 4. Godina se deli na dvaneaest pravilnih meseci koji su konačno usvojeni u Gregorijanskom kalendaru.

6.3.3 Istorija Julijanskog kalendara

Godina -45 se zvala "godina konfuzije", zato što je te godine Julije Cezar ubacio 90 dana da bi doveo mesece Rimskog kalendara natrag na tradicionalno mesto u odnosu na godišnja doba. To je bio prvi Cezarov korak reforme kalendara koji je pošao naopako. Mada je pre-Julijanski kalendar bio lunarni kalendar po inspiraciji, njegovi meseci nisu više pratili mesečeve mene a godina je izgubila korak sa ciklusom godišnjih doba. Prateći savet Sosigenesa, aleksandrijskog astronoma, Cezar je napravio sunčev kalendar sa dvanaest meseci fiksne dužine i mogućnost za jedan umetnut dan koji se može dodati svake četvrte godine. Kao rezultat, srednja dužina godine Julijanskog kalendara je bila 365.25 dana. Ovo je bilo saglasno sa tropskom godinom kakva je bila poznata u to vreme.

Posle Cezarove smrti, rimski kalendarski autoriteti pogrešno su primenili pravilo prestupne godine, sa rezultatom da je svaka treća, a ne četvrta godina bila interkalarna. Mada ne postoje detaljni dokazi, uglavnom se veruje da je imperator Avgust ispravio situaciju izostavljajući umetanje od Julijanske godine -8 do +4. Posle toga je Julijanski kalendar počeo da funkcioniše kako je planirano.

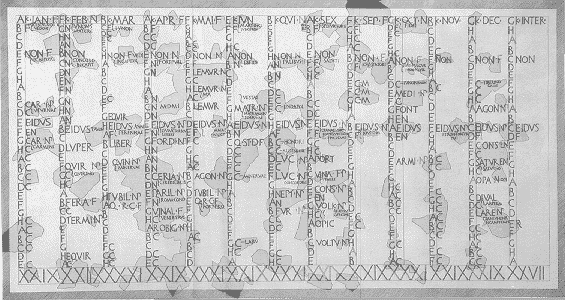
Kroz srednji vek upotreba Julijanskog kalendara se razvila i dobila je neke lokalne osobenosti koje nastavljaju da predstavljaju zamku za neoprezne istoričare. Postojale su razlike u početnoj epohi za računanje godina, datumu početka godine i metode za određivanje dana u mesecu. Ne samo da su varirali sa vremenom i mestom već i sa svrhom. Različite konvencije su se upotrebljavale za razne crkvene zapise, finansijske transakcije i ličnu prepisku.

Cezar je odredio 1. januar kao početak godine. Pa ipak, cvetale su i druge konvencije u raznim vremenima i na raznim mestima. Najpopularnije zamena su bile 1. mart, 25. mart i 25. decembar. Ovo je nastavljalo da pravi probleme istoričarima, pošto je, na primer, 28. februar +998. zapisan u gradu u kome godina počinje 1. marta, isti dan kao 28. februar +999. grada u kome godina počinje 1. januara.

Dani u mesecima su se prvobitno računali od označenih tačaka podela u mesecu: Kalends, Nones i Ides. Kalenda je prvi dan meseca. Ide su trinaesti dan u mescu, izuzev u martu, maju, julu i oktobru, kada je petnaesti dan. None su uvek osmi dan pre Ida (videti Tabelu 6.3.1). Dani koji padaju između ovih tačaka podele su označeni brojanjem unatrag od dolazeće tačke podele. Umetanje je bilo ponavljanje dana VI Kalendi Marta, tj. umetanje dana VI Kalende Marta (24. februar) i VII kalende Marta (23. februar).

U jedanaestom stoleću ušlo je u upotrebu neprekidno brojanje dana od početka meseca. Lokalne razlike su se ipak nastavile uključujući brojanje dana od datuma komemoracije lokalnih svetaca. Zvanično uvođenje i širenje Gregorijanskog kalendara proizvelo je usvajanje uniformnog standarda za zapisivanje datuma.

7.1 GREGORIJANSKI KALENDAR - NOVI STIL

S obzirom na tačnost sa kojom je urađen i na dobru samerljivost sa godišnjim ciklusom, ovom kalendaru dajemo posebno mesto. Gregorijanski kalendar služi danas kao međunareodni standard za građansku upotrebu. Jasno je da je nastao kao poboljšanje toka i rasporeda ceremonijalnih događaja u praksi Rimokatoličke i Protestantske crkve.

Akumulacija razlike dužine tropske godine i julijanske kalendarske godine od 0.0076 dana godišnje, dovela je do toga da se već u šesnaestom veku nakupi 10 dana, što je u odnosu na red prirodnih događaja bilo primetno. Ovaj problem je posebno tangirao Rimokatoličku crkvu, jer se činilo da će doći vreme da se Uskrs slavi u leto.

Papa Pavle III je regrutovao nekoliko astronoma, prvenstveno jezuitu Cristopher-a Clavius-a ^* da predlože rešenje za poboljšanje kalendara. Oni su predložili reformu kalendara u skladu sa rešenjem koje je dao astronom i fizičar Luigi Lilio ^** nešto ranije. Kada je izabran Ugo Buoncompagni za Papu (Grgur XIII), nasledio je različite preporuke za reformu kalendara. Odlučio se za Clavius-ov predlog i 24.02.1582. godine je izdao papsku bulu Inter Gravissimas naglašavajući time da je to izbor ''Između ...'' što i jesu početne reči te bule.

Sama reforma se sastojala u sledećem:

1. izostavlja se 10 dana iz kalendarskog brojanja i nalaže se da posle četvrtka, 4. oktobra 1582. bude petak, 15. oktobar 1582.
2. menja se pravilo za prestupne godine utoliko što više nisu prestupne godine koje označavaju stoleća (stotine) ukoliko broj stoleća nije deljiv sa 4 bez ostatka.
3. položaj dodatnog dana u prestupnoj godini pomera sa dana pre 25. februara (ranije su najčešće bila 2 24. februara!) na dan posle 28. februara, tj. pojavljuje se 29. februar.

Isto tako, ova reforma nije dovela do stabilizacije ''položaja'' datuma prolećne ravnodnevice, čime bi se pojednostavio račun pokretnih praznika. Pretpostavlja se da reforma, koja je to predviđala, nije usvojena iz (nekih) političkih razloga.

Svi ostali kalendari, koji su danas u upotrebi, ograničeni su na pojedine religije i kulture. Prednost Gregorijakskog kalendara bila je njegova iskoristivost i za svetovne i za duhovne potrebe i jednostavnost u primeni.

Tako je godina 2000. prestupna godina, dok 1700.,1800. 1900. i 2100. nisu prestupne godine.... Ova pravila se mogu primeniti na vremena pre Gregorijanske reforme čime se stvara proleptički Gregorijanski kalendar. U ovom slučaju, godina 0, (1 godina p.n.e.) se smatra prestupnom godinom. Gregorijanski kalendar je, prema tome, zasnovan na ciklusu od 400 godina, koji sadrži 146097 dana. Pošto se 146097 može podeliti sa sedam bez ostatka, Gregorijanski gradanski kalendar se ponavlja tačno posle 400 godina. Deljenje 146097 sa 400 dovodi do srednje dužine od 365.2425 dana u kalendarskoj godini, koja je bliska srednjoj vrednosti dužine tropske godine. Poređenje sa ranijom jednačinom otkriva da Gregorijanski kalendar akumulira grešku od jednog dana za 2500 godina. Mada su predložena razna podešavanja sistema prestupne godine nijedno nije zvanično prihvaćeno.

U svakoj godini, datumi su određeni prema broju dana od početka meseca. Red meseci i broj dana u mesecu je usvojen iz Julijanskog kalendara .

8.1 CRKVENA PRAVILA

Uporišne tačke crkvenih kalendara (Hrišćanskih crkvi) su trenuci (datumi) tzv. ''pokretnih'' i ''stalnih'' praznika. Božić je glavni ''nepokretni'' praznik, a datumi većine drugih pokretnih praznika su određeni u odnosu na Uskrs (Vaskrs). Pokretni praznici su u vreme Bogojavljenja nedelje koje se računaju od Božića i praznika Bogojavljenja.

Nažalost, zbog izuzetno izraženih autonomnih interesa, u ovom delu primene kalendara postoji blagi haos, pa ćemo ovde dati jedan presek onoga što se danas može nazvati skoro sigurnim.

U izvornim računima određeno je da je Uskrs u nedelju koja prati prvi ''crkveni'' pun Mesec posle martovskog ekvinokcija. Ovo ne treba mešati sa popularnim pojmom da Uskrs pada u prvu nedelju posle punog Meseca koji prati prolećni ekvinocij. Kao prvo, prolećni ekvinocij ne pada obavezno 21. marta. Osim toga, crkveni pun Mesec nije isto što i astronomski pun Mesec - on se zasniva na tabelama koje ne uzimaju u obzir kompleksnost kretanja Meseca. Kao rezultat, datum crkvenog punog Meseca može znatno da se razlikuje od stvarnog punog Meseca. Gregorijanski sistem prestupne godine sprečava da razlika između ''crkvenih'' mesečevih tabela i astronomskih podataka o fazama Meseca dostigne više od 5 dana. Međutim, tih nekoliko dana i različiti kalendarski sistemi su dovoljni da izazovu priličnu zbrku.

Prema crkvenim tablicama crkveni pun Mesec je definisan kao četrnaesti dan tablica meseca, dok dan 1. odgovara crkvenom mladom Mesecu. Tablice se zasnivaju na Metonovom ciklusu, u kome 235 srednjih sinodičkih meseci traje 6939.688 dana. Pošto je devetnaest Gregorijanskih godina 6939.6075 dana, trenuci mesečevih mena će se ponoviti skoro istog datuma devetnaest godina kasnije.

Da se spreči nakupljanje razlike od 0.08 dana po Metonovom ciklusu, tablice sadrže popravke za sinhronizaciju na dugim vremenskim intervalima. Komplikacije se pojavljuju i zato što su tabelarni meseci od 29 ili 30 dana. Kompletan sistem sadrži period od 5700000 godina od 2081882250 dana, što je jednako 70499183 meseci. Posle ovog perioda, datumi Uskrsa se ponavljaju.

9.1 JEVREJSKI KALENDAR

Jevrejski kalendar je lunisolarni kalendar i danas zasnovan više na proračunima nego na posmatranjima. Ovaj kalendar je zvanični kalendar Izraela i liturgijski kalendar jevrejske vere. U principu početak svakog meseca je određen mladim Mesecom iz tabele ( molad) koja je zasnovana na usvojenoj srednjoj vrednosti mesečevog ciklusa (lunacija). Da bi obezbedili da se verski praznici pojavljuju u odgovarajućoj sezoni, meseci su umetnuti prema Metonovom ciklusu, u kome se 235 lunacija pojavljuju u 19 godina. Po tradiciji, dani u nedelji su označeni brojevima, a samo sedmi dan, Shabbat, ima ime. Dani se računaju od zalaza do zalaza, tako da 1. dan počinje zalazom u subotu i završava se pri zalazu u nedelju. Shabbat počinje pri zalazu u petak i završava se pri zalazu u subotu.

9.2 Istorija Jevrejskog kalendara

Obično se smatra da je kodifikovani Jevrejski kalendar kakav mi danas poznajemo nastao 4119 A.M. (+359), mada je tačan datum nepoznat. U to vreme je patrijarh Hillel II, kršeći tradiciju, širio pravila za računanje kalendara. Pre ovog vremena kalendar se smatrao tajnom naukom verskih vlasti. Precizniji detalji Hillelovog kalendara nisu došli do nas, ali se uglavnom smatra da je sadržao pravila ubacivanja u devetnestogodišnjim ciklusima. Do desetog veka n.e. postojala su neslaganja o pravim godinama za ubacivanje i o početnoj epohi za računanje godina.

Informacije o kalendarskoj praksi pre Hillela su fragmentarne i često kontradiktorne. Najraniji dokumenti pokazuju da je kalendar zasnovan na posmatranjima mesečevih mena. Pošto Biblija spominje sezone praznika, mora da je postojalo ubacivanje. Verovatno je postojao sukob u razvoju kalendarskih praksi.

Izgnanstvo iz Vavilona, u prvoj polovini šestog stoleća p.n.e., je dosta uticalo na Jevrejski kalendar. Ovo se i danas vidi po nazivima meseca. Vavilonski uticaj je možda takođe doveo do prakse interkalacije, ubacivanja, prestupnih meseci.

Za vreme Sanhedrina ^* , komisija Sanhedrina se sastajala da proceni izveštaj o posmatranju mesečevog srpa. Kada se nije moglo posmatrati, novi mesec je počinjao 30 dana posle početka prethodnog meseca. Na odluku o ubacivanju uticalo je, (mada ga nije potpuno odredilo) stanje vegetacije i život životinja.

9.3.1 Pravila

Godine se računaju od Ere postanka, ili Era Mundi, koja odgovara 7. oktobru -3760. po Julijanskom proleptičkom kalendaru. Svaka godina se sastoji od dvanaest ili trinaest meseci koji se sastoje iz 29 ili 30 dana. Jedan umetnuti mesec se uvodi u godinama 3, 6, 8, 11, 14, 17 i 19 u devetnaestogodišnjem ciklusu od 235 lunacija. Početna godina kalendara, A.M. (Anno Mundi) 1, je godina 1. devetnaestogodišnjeg ciklusa. Kalendar za date godine je ustanovljen određivanjem dana nedelje 1. Tishri (prvi dan Rosh Hashanah ili Nova Godina) i brojeva dana u godini. Godine su određene prema broju dana u godini (pogledajte tabelu 9.1.1)

Meseci Heshvan i Kislev imaju promenljivu dužinu da bi zadovoljili zahteve za dužinu godine (pogledajte tabelu 9.1.1.). U prestupnim godinama, mesec Adar od 29 dana, je označen sa Adar II, a njemu prethodi umetnuti mesec Adar I od 30 dana. Za proračune kalendara, dan počinje u 6h posle podne što je označeno sa časovi. časovi su podeljeni na 1080 halakima; tako je jedan helek 31/3 sekunde. (Termonologija je objašnjena u Tabeli 9.1.3). Kalendarski proračuni se odnose na meridijan Jerusalima, 2 časa 21 minuta istočno od Greenwich-a.

9.3.2 Određivanje 1. Tishri-a

Kalendarska godina počinje sa prvim danom Rosh Hashanaha (1. Tishri). Određeno je danom Tishri molad i sa četiri pravila odlaganja ( dehiyyot). Dehiyyot može da odloži 1. Tishri jedan ili dva dana posle molada. Utabličeni mladi meseci ( maladot) se računaju od Tishri molad godine 1. A.M., što se desilo 2. dana u 5 h, 204 halakima (tj., 11:11:20 posle podne u nedelju 6. oktobra -3760. Julijanskog proleptičkog kalendara). Usvojena vrednost srednje lunacije je 29 dana, 12 časova, 793 halakima (29.530594 dana) Da bi se izbegle greške odbacivanja i zaokruživanja, proračuni se vrše u halakima, a ne u decimalima dana, pošto je usvojena lunaciona konstanta tačno izražena u halakima.

Lunacione konstante potrebne za račun su prikazane u Tabeli 9.1.4. Oduzimanjem nedelja, ove konstante daju pomeranje dana u nedelji koje se pojavljuje posle svakog ciklusa.

Primer 1 Nađi dan u nedelji i vreme Tishri molad 2. A.M.

Pošto je to obična godina, 1 A. M. ima dvanaest lunacija. Prema tome, pomeranje dana u nedelji u toku dvanaest lunacija se može dodati na molad epohe:

Dehiyyoti su:

1. Ako Tishri molad pada 1., 4., ili 6. dana, 1. Tishri je odložen za jedan dan.
2. Ako se Tishri molad pojavljuje u ili posle 18 h (tj., u podne), tada je 1. Tishri odložen za jedan dan. Ako ovo prouzrokuje da 1. Tishri pada 1., 4. ili 6. dana tada je on odložen za još jedan dan da bi zadovoljio dehiyyah (a).
3. Ako Tishri molad neke obične godine (tj., godine od 12 meseci) pada 3. dana posle 9 h, 204 halakima, tada je 1. Tishri odložen za dva dana do 5. dana, zadovoljavajući tako dahiyyah (a).
4. Ako prvi molad posle prestupne godine pada na drugi dan u ili posle 15 časova, 589 halakima, tada je 1. Tishri odložen jedan dan, do 3. dana.

Primer 2 Nađi dan 1.Tishri 5760. A.M.

Pošto je početna epoha, 5759 godina prošla i sadrži 303 devetnaestogodišnja ciklusa i dve godine, obe ove godine su obične godine. Lunacione konstante koje su ranije date (sa eliminisanim celim nedeljama) daju pomeranje dana u nedelji, koje se dodaje na molad epohe:

9.3.3 Razlozi za dehiyyot

Dehiyyah (a) sprečava da se Hoshana Rabba (21. Tishri) desi na Shabbat i sprečava Yom Kippur (10. Tishri) da se desi na dan pre ili posle Shabbat-a.

Dehiyyah (b) je veštački proizvod stare prakse da svaki mesec počinje od opažanja mesečevog srpa. Pretpostavlja se da ako se molad (tj., mesečeva konjunkcija) pojavljuje posle podne, mesečev srp se ne može opaziti do 6 posle podne, što će onda biti sledećeg dana. (Za dalje informacije o vidljivosti mesečevog srpa, pogledajte odeljak 10.1.2)

Dehiyyah (c) sprečava običnu godinu da pređe 355 dana. Ako se Tishri molad neke obične godine pojavi u utorak u ili posle 3:11:20 popodne novi Tishri molad će se pojaviti u ili posle podne u subotu. Prema dehiyyahu, 1. Tishri sledeće godine je odložen do nedelje, a to izaziva u slučajevima dehiyyaha dalje odalganje do ponedeljka. Ovo daje običnu godinu od 356 dana, ali odlaganje 1.Tishria od utorka do četvrtka daje godinu od 354 dana.

Dehiyyah (d) sprečava da prestupna godina bude kraća od 383 dana. Ako je Tishri molad koji prati prestupnu godinu u ponedeljak, u ili posle 9:32:43 1/3 popodne, prethodni Tishri molad (trinaest meseci ranije) pojavljuje se u utorak u ili posle podne. Prema tome, po dehiyyahu (b) i (a), 1. Tishri kojim počinje prestupna godina je odložen do četvrtka. Da se spreči godina od 382 dana, dehiyyah (d) za jedan dan odlaže početak obične godine.

Pomeranje dana u nedelji posle trinaest lunacija je 05-21-589. Ako se Tishri molad prestupne godine desi 4. u 20h 500 halakima, sledeći Tishri molad će se desiti 3. u 18h 9 halakima. Zbog dehiyyaha (b) 1. Tishri prestupne godine će biti odložen za dva dana do 6. dana. Zbog dehiyyaha (c) 1. Tishri sledeće godine će biti odložen za dva dana do 5. dana. Razlika od šest dana je karakteristika pravilne godine, tako da Heshvan ima 29 dana a Kislev 30 dana.

10.1 ISLAMSKI KALENDAR

Islamski kalendar je isključivo mesečev kalendar u kome meseci odgovaraju mesečevom ciklusu faza. Kao razultat, ciklus od 12 lunarnih meseci se vraća unazad kroz godišnja doba u periodu od oko 33 godine. Za verske svrhe, muslimani su počinjali mesece sa prvom vidljivošću mesečevog srpa posle konjunkcije. Za građanske svrhe često se koristi kalendar koji aproksimira mesečev fazni ciklus.

Nedelja se sastojala od sedam dana od kojih svaki počinje od zalaza Sunca. Dani nedelje su označeni brojem, sa 1. danom koji počinje pri zalazu u subotu i završava se pri zalazu u nedelju. 5. dan koji se zove Juma je dan za zajedničke molitve. Nasuprot subotnjem danu Hrišćana i Jevreja, Juma nije dan odmora. Juma počinje sa zalazom Sunca u četvrtak i završava se sa zalazom u petak.

10.1.1 Istorija Islamskog kalendara

Islamskog kalendar, kao lunarni kalendar bez umetanja meseci dao je Prorok u Kuranu (sura IX, stih, 36-37) i u njegovoj službi ''Oproštajno hodočašće''. To je bilo odvajanje od lunisolarnog kalendara arapskog sveta u kome su se meseci zasnivali na prvom viđenju srpa, a jedan umetnut mesec se dodavao ako je to izgledalo potrebno.

Kalifu Umaru I. se pripisuje da je uspostavio Hijra Eru 17. A.H. Ne zna se kako je utvrđen početni datum. Pa ipak, proračuni pokazuju da se astronomski mlad Mesec (tj., konjunkcija) pojavio 14 jula +622. godine (pretpostavljajući ΔT = 1.0 h), tako da se opažanje srpa desilo verovatno 16. jula uveče.

10.1.2 Pravila

Godine od dvanaest meseci se računaju od Hijra ere, koja je spomen bekstvu Proroka (Muhameda) i njegovih sledbenika iz Meke u Medinu. Ova epoha 1. A.H. (Anno Hegirae) Muharam 1., astronomi uglavnom smatraju (Neugebauer, 1975.) da pada u četvrtak, 15. juli +622 (Julijanski kalendar). To se zove astronomska Hijra epoha. Hronološke tablice (primer, Mayr i Spuler, 1961, Freeman-Grenville, 1963.) obično koriste petak 16. juli koji je označio građansku epohu. U oba slučaja islamski dan počinje prethodnog dana pri zalazu Sunca.

Za verske svrhe, svaki mesec počinje u principu sa prvim opažanjem mesečevog srpa posle mladog meseca. Ovo je posebno važno za ustanovljavanje početka i kraja Ramadana. Naravno da su vremenske prilike dovodile do visoke nepouzdanosti određivaja ovog trenutka, pa je uvedena praksa da novi mesec može da se objavi 30 dana posle početka prethodnog meseca. Mada su se koristile razne procedure predviđanja i određivanja prvog opažanja (videti odeljak 10.1.2), one su uvek imale sumnjiv status. U praksi, postoji razilaženje između zemalja, religioznih vođa, naučnika o tome da li je dovoljno osloniti se na posmatranja, koja su podložna grešci, ili da se upotrebe proračuni, koji mogu biti zasnovani na lošim modelima.

Hronolozi pri proučavanju islamske istorije upotrebljavaju kalendar sa 30-godišnjim ciklusom. U ovom tabličnom kalendaru, postoji 11 prestupnih godina u ciklusu od 30 godina. Meseci označeni neparnim brojevima imaju 30 dana, a meseci označeni parnim brojevima imaju 29 dana, sa tridesetim danom dodatim dvanaestom mesecu Dhu al-Hijjah (videti Tabelu 10.1.1). Kao prestupne godine označene su godine ciklusa 2., 5., 7., 10., 13., 16., 18., 21., 24., 26. i 29. Ova vrsta kalendara se koristi u nekim islamskim zemljama i kao građanski kalendar, mada se ponekad neke druge godine koriste kao prestupne godine. Srednja dužina meseca tridesetogodišnjeg utabličenog kalendara je manja za 2,9 sekunde od sinodičkog meseca.

10.1.3 Vidljivost mesečevog srpa

Pod opitmalnim uslovima, mesečev srp se može videti oko 15,4 h posle astronomskog mladog Meseca (tj., konjunkcije), ali obično se ne vidi prvih 24 h. Vavilonski astronomi su bili prvi koji su razvili metode za proračunavanje prve vidljivosti, mada se tabele koje su preostale ne odnose direktno na ovaj račun. Najranije poznate tabele vidljivosti su al-Khwarizmi-jeve (astronom iz devetnaestog veka iz Bagdada). Ove tabele, i mnoge posle njih, su osnovane na indijskim kriterijumima da će Mesec biti vidljiv ako je lokalni časovni ugao Meseca pri zalazu Sunca jednak ili manji od 78°. Sa razvojem islamske astronomije, razvijeni su još kompleksniji kriterijumi od strane islamskih astronoma.

Moderni modeli za predviđanja prve vidljivosti uključuju nebesku mehaniku, sfernu astronomiju, selenologiju, atmosfersku fiziku i oftalmologiju. Bruin, 1977. je bio prvi koji je pripremio ovakav model. Ilyas, 1984, videvši da se islamski kalendar upotrebljava širom sveta, je uveo koncept " International Lunar Dateline", zapadno od koga Mesec treba da je vidljiv pri dobrom uslovima posmatranja. Dalje teoretske radove je vršio Schaefer, 1988. Doggett, Seidelmann i Schaefer, 1988. i Doggett i Schaefer, 1989. su organizovali opsežne posmatračke programe.

11.1 INDIJSKI KALENDAR

Kao rezultat reforme kalendara 1957. n.e., indijski Nacionalni kalendar je formalizovao lunisolarni kalendar u kojem se prestupne godine podudaraju sa prestupnim godinama u Gregorijanskom kalendaru (Komitet za reformu kalendara, 1957.). Pa ipak, početak je Saka Era, tradicionalna epoha indijske hronologije. Mesecima su data tradicionalna imena i oni su pomereni u odnosu na početak Gregorijanskih meseci (videti Tabelu 11.1).

Osim što je uspostavio građanski kalendar Komitet za reformu kalendara je postavio pravila za verske kalendare, koja zahtevaju račune kretanja i položaja Sunca i Meseca. Tablice verskih praznika je pripremilo Metereološko odeljenje i objavljuju se jednom godišnje u The Indian Astronomical Ephemris.

Uprkos pokušaja da se uspostavi jedinstven kalendar za celu Indiju, postoje razne varijacije. Gregorijanski kalendar se i dalje koristi u administrativne svrhe, a praznici se još uvek određuju prema pokrajinama, religiji i tradiciji.

11.1.1 Istorija Indijskog kalendara

Istorija kalendara u Indiji je veoma složena usled kontinuiteta indijske civilizacije i uticaja raznih kultura. Sredinom 50-ih kada je Komitet za reformu kalendara naparavio snimak stanja, postojalo je u upotrebi oko 30 kalendara za verske praznike Indusa, Budista i Jainista. Neki od njih su se koristili i za građanske potrebe. Ovi kalendari su bili osnovani na zajedničkim principima, mada su imali lokalne karakteristike određene davno ustanovljenim običajima i astronomskom praksom lokalnih tvoraca kalendara. Osim toga, muslimani u Indiji su koristili Islamski kalendar, a indijska vlada je koristila Gregorijanski kalendar za administrativne svrhe.

Rane aluzije na lunisolarni kalendar sa ubačenim mesecima su nađene u epu Rg Veda, koja datira dve hiljade godina p.n.e. Literatura od 1300. p.n.e. do 300. n.e. daje bliže informacije. Petogodišnji lunisolarni kalendar usklađivao je sunčeve godine sa sinodičkim i sideričkim mesecima.

Indijska astronomija je pretrpela opštu reformu u prvih nekoliko stoleća n.e., kada je postao poznat napredak u vavilonskoj i grčkoj astronomiji. Usvojene su nove konstante i modeli za kretanje Sunca i Meseca u tradicionalnoj kalendarskoj praksi. To je bilo izneto u astronomskim spisima tog doba poznatim kao Siddhantas, od kojih su mnogi nestali. Surya Siddhanta, koji je nastao u četvrtom stoleću, a ažuriran je u sledećim stolećima, uticao je na tvorce kalendara u Indiji sve do, a i posle reforme kalendara 1957. n.e.

Pingree, 1978 daje pregled razvoja matematičke astronomije u Indiji. Mada se ne bavi direktno kalendarima, ovaj materijal je neophodan za potpuno razumevanje istorije indijskih kalendara.

11.1.2 Pravila za građansku upotrebu

Godine se računaju od Saka Ere; Smatra se da 1. Saka počinje sa ekvinokcijem 79. n.e. Reformisan indijski kalendar počinje sa Saka Erom 1879. što odgovara 22. martu 1957. n.e. Normalne godine imaju 365 dana a prestupne 366 dana. U prestupnoj godini jedan umetnut dan se dodaje na kraj kalendara. Da bi odredili prestupne godine, prvo dodajte 78 na Saka godinu. Ako se zbir može podeliti sa 4, godina je prestupna, osim ako je zbir multipl od 100. Tabela 11.1.1 prikazuje spisak meseci i njihov odnos prema mesecima Gregorijanskog kalendara.

Zadržana je nedelja od sedam dana, potpuno povezana sa zapadnom nedeljom. Dani teku od ponoći do ponoći.

11.1.3 Osnove verskog kalendara

Verski praznici su određeni lunisolarnim kalendarom koji se zasniva na računima stvarnih položaja Sunca i Meseca. Kao što će se videti, većina praznika su određenog mesečevog datuma ( tithis); retko su dati za određeni sunčev datum. Metode koje su ovde predstavljene preporučio je Komitet za reformu kalendara, 1957. One služe kao osnova za kalendar objavljen u The Indian Astronomical Ephemeris. Pa ipak, mnogi lokalni tvorci kalendara upotrebljavaju tradicionalne astronomske koncepte i formule, a neke od njih potiču još iz 1500.

Komitet za reformu kalendara je nameravao da uskladi tradicionalnu kalendarsku praksu sa modernim astronomskim konceptima. Prema njihovim predlozima, precesija se uzima u obzir, a proračuni položaja Sunca i Meseca su zasnovani na tačnim modernim metodama. Svi astronomski proračuni se obavljaju u odnosu na Centralnu stanicu na istočnoj longitudi od 82°30′ i severnoj latitudi od 23°11′. U verske svrhe sunčevi dani se računaju od izlaza do zalaza Sunca.

Sunčev mesec je definisan kao interval koji je potreban sunčevoj prividnoj longitudi da se poveća za 30°, što odgovara prolazu Sunca kroz zodijački znak ( rasi). Početni mesec godine Vaisahka, počinje kada je stvarna longituda Sunca 23°15′ (videti Tabelu 11.1.2). Pošto je zemljina orbita eliptična, dužina meseca varira od 29.2 do 31.2 dana. Svi kratki meseci se javaljaju u drugoj polovini godine oko vremena prolaska Zemlje kroz perihel.

Lunarni meseci su mereni od jednog mladog Meseca do drugog (mada neke grupe računaju od punog Meseca). Svakom lunarnom mesecu je dato ime sunčevog meseca u kome počinje lunarni mesec. Pošto je većina lunacija kraća od sunčevog meseca, postoje sunčevi meseci u kojima se pojave dva mlada Meseca. U ovom slučaju, oba lunarna meseca nose isto ime, ali je prvi mesec opisan prefiksom adhika, ili umetnut. Takva godina ima 13 lunarnih meseci. Adhika meseci se pojavlju svake dve ili tri godine prateći model opisan Metonovim ciklusom ili još kompleksnije ciklusom mesečevih mena.

Ređe će se pojaviti godina u kojoj će kratak sunčev mesec proći bez mladog meseca. U ovom slučaju, ime sunčevog meseca se ne pojavljuje u kalendaru za tu godinu. Takav nepravilan mesec (ksaya) se može pojaviti samo u mesecima blizu prolaska Zemlje kroz perihel. Kao kompenzacija, mesec u sledećoj polovini godine će imati dva puna Meseca, tako da će godina i dalje imati dvanaest lunarnih meseci. Ksaya meseci mogu biti u razmaku od devetnaest godina, a mogu se pojaviti i tek posle 141 godine.

Lunacije su podeljene na 30 tithis ili lunarnih dana. Svaki tithi je definisan vremenom koje je potrebno da se longituda Meseca poveća za 12° više od longitude Sunca. Tako dužina thitia može da varira od oko 20h do skoro 27h. U toku faze povećavanja, thitisi se broje od 1 do 15 sa oznakom Sukla. Thitisi u fazi smanjivanja su označeni sa Krsna i opet se broje od 1 do 15. Svakom danu je dodeljen broj thitia koji je u toku u vreme izlaza Sunca. Ponekada kratak thiti će početi posle izlaza Sunca i završiti se pre sledećeg izlaza. Slično, dugi thiti može da zahvati dva izlaza. U prvom slučaju, broj je izostavljen iz brojanja dana. U drugom se redni broj dana prenosi u sledeći dan.

12.1 KINESKI KALENDAR

Kineski kalendar je lunisolarni kalendar zasnovan na proračunima položaja Sunca i Meseca. Meseci od 29 i 30 dana počinju na dane astronomskih mladih Meseca, sa jednim umetnutim-interkalarnim mesecom koji se dodaje svake dve ili tri godine. Pošto je kalendar zasnovan na pravim položajima Sunca i Meseca, tačnost kalendara zavisi od tačnosti astronomskih teorija i proračuna.

Mada se Gregorijanski kalendar koristi u Narodnoj republici Kini u administrativne svrhe, tradicionalni Kineski kalendar se koristi za određivanje praznika i određivanje vremena za poljoprivredne aktivnosti u provinciji. Kineski kalendar takođe upotrebljavaju kineske zajednice širom sveta.

12.1.1 Istorija Kineskog kalendara

U Kini je kalendar bio sveti dokument, sponzorisan i obnarodovan od vladara. Više od 2000 godina Astronomski biro je održavao astronomska posmatranja, proračunavao astronomske događaje kao što su pomračenja, objavljivao astronomska predviđanja i održavao kalendar. Uspešan kalendar nije značio samo zadovoljenje praktičnih potreba već je i potvrđivao slaganje Neba sa Dvorom imperije.

Analize preostalih astronomskih zapisa opisuju proročki Kineski lunisolarni kalendar, sa ubacivanjem lunarnih meseci, unatrag čak do dinastije Shang u četrnaestom stoleću p.n.e. Razne sheme umetanja su se razvile u ranim kalendarima, uključujući 19-ogodišnje i 76-godišnje fazne cikluse koji su postali poznati na zapadu kao Metonov ciklus i Callipic-ov ciklus ^*.

Iz najranijih zapisa se vidi da je početak godine bio pri mladom Mesecu blizu zimskog solsticija. Izbor meseca kojim je počinjala godina varirao je sa mestom i vremenom. Pri kraju drugog stoleća p.n.e. ustanovljena je prksa, koja se nastavlja i danas, da zimski solsticij bude u 11. mesecu. Ova reforma je uvela i sistem interkalacije - umetanja gde su datumi mladog Meseca poređeni sa 24 sunčeva člana (videti odeljak dalje). Ipak, proračuni su bili zasnivani na srednjim kretanjima koja su proizlazila iz određenih odnosa. Neujednačenost kretanja Meseca je bila uzeta u obzir još u sedmom veku n.e., ali sunčeva srednja longituda je korišćena za proračune sunčevih članova sve do 1644.

Godine su računate iz sukcesija era koje su ustanovili u to vreme vladajući imperatori. Mada bi dolazak jednog imperatora značio otpočinjanje nove ere, imperator je mogao da proglasi novu eru i za vreme svoje vladavine. Uvođenje nove ere je bio pokušaj da se ponovo uspostave pokidane veze između Neba i Zemlje, koju je predstavljao imperator. Prekid je mogao da bude predstavljen bolešću imperatora, pojavama elementarnih nepogoda, ili propustom astronoma da predvide nebeske događaje kao što je na primer pomračenje. U poslednjem slučaju, nova era je bila znak uvođenja novih astronomskih ili kalendarskih modela.

Seksagezimalni sistem je korišćen za brojanje godina, meseci, dana i delova dana koristeći skup nebeskih stabala i zemaljskih grana opisanih ranije. Korišćenje ciklusa od 60 dana je prisutno u najranijim astronomskoim zapisima. Nasuprot tome, korišćenje ciklusa od 60 godina je uvedeno u prvom stoleću n.e. ili stoleće ranije (Tung, 1960; Needham, 1959.). Mada je brojanje dana prestalo u svakodnevnoj upotrebi, još uvek se tabliči u kalendarima. Početna godina (jia-zi) jednog od ciklusa godina počela je 2. februara 1984., koji je treći dan (bing-yin) ciklusa dana.

Zapadne (pre Kopernika) astronomske teorije su uvedene u Kinu posredstvom Jezuita misionara u sedamnaestom stoleću. Postepeno, postali su poznati još moderniji zapadni koncepti. Posle revolucije 1911, tradicionalna praksa računanja godina prema dolasku imperatora na presto je ukinuta.

12.1.2 Pravila

Ne postoji posebna početna epoha za računanje godina. U istorijskim spisima datumi su specifikovani brojanjem dana u ciklusima sa osnovom šest i brojanjem godina iz redosleda era koje su ustanovili vladajući monarsi (videti kasniji odeljak).

Ciklus od 60 godina se satoji od imena koja su stvorena uparivanjem imena iz liste od deset Nebeskih stabala sa imenima iz liste od dvanaest Zemaljskih grana, prateći red dat u Tabeli 12.1. Imena nebeskih stabala se ne prevode (kineski znaci), dok su Zemaljske grane imena 12 životinja. Posle šest ponavljanja ''stabla'' i pet ponavljanja ''grana'', kompletni ciklus parova je završen, počinje novi ciklus. Početna godina (jia-zi) jednog od ciklusa počela je 2. februara 1984.

Dani se računaju od ponoći do ponoći. Prvi dan kalendarskog meseca je dan u kome je proračunato da će se pojaviti astronomski mlad Mesec (konjunkcija). Pošto je prosečni razmak između sukcesivnih mladih meseca približno 29.53 dana, meseci su od 29 ili 30 dana. Meseci su određeni brojevima od 1 do 12. Kada se dodaje umetnut mesec on nosi broj prethodnog meseca., ali je označen kao umetnut. Jedna obična godina od dvanaest meseci ima 353, 354 ili 355 dana; prestupna godina ima trinaest meseci je 383, 384 ili 385 dana.

Uslovi za dodavanje meseca su određeni intervalom pojave mladog Meseca u odnosu na delove tropske godine. Tropska godina je podeljena na 24 sunčeva člana, u segmente od 15° sunčeve longitude. Ovi delovi su upareni sa dvanaest deobnih članova (Jieqi) i dvanaest glavnih članova ( Zhogqi), kao što je prikazano u Tabeli 12.1.3 Ovi članovi su označeni brojevima i data su im imena metereološka ili sezonska. U primerima koji slede radi pojednostavljenja članovi su označeni sa S i P koje prati broj. Usled eliptičnosti zemljine orbite razmak između sunčevih članova se menja sa godišnjim dobima.

Referentni radovi daju razna pravila za ustanovljavanje dana Nove godine i za umetanje u lunisolarni kalendar. Pošto je kalendar u početku zasnovan na pretpostavci da je kretanje Sunca jednako po godišnjim dobima, objavljena pravila su često neadekvatna za specijalne slučajeve.

Sledeća pravila se trenutno koriste za osnovu kalendara.

1. Prvi dan meseca je dan kada se pojavljuje mlad Mesec.
2. Obična godina ima dvanaest lunarnih meseci; interkalarna godina ima trinaest lunarnih meseci.
3. Zimski solsticij (član P-11) uvek pada u 11. mesec.
4. U interkalarnoj godini, mesec u kome nema glavnog člana je umetnut mesec. On je dobio broj prethodnog meseca, sa oznakom umetanja. Ako dva meseca godine sa umetanjem ne sadrže glavni član, samo se prvi mesec posle zimskog solsticija smatra umetnutim.
5. Proračuni su dati za istočni meridijanu na 120°.

Broj meseci obično odgovara broju glavnih članova koji se pojavljuju u toku meseca. U retkim slučajevima, postoje meseci koji imaju dva glavna člana, što daje rezultat da neumetnut mesec neće imati glavni član. Ovi slučajevi se mogu rešiti striktnom primenom pravila 2 i 3. Ova atipična situacija je data u 2. primeru.

Primer 1 (tipičan slučaj): Nađi Greogorijanski datum Kineske Nove godine 1990.

Zimski solsticij (glavni član 11) se pojavljuje 22. decembra 1990. a Nova godina na ili pre tog datuma je 17. decembra. Odavde možemo sastaviti sledeću tabelu pojava:

Kineska nova godina pada 15. februara. U ovom periodu nema umetnutih (interkalarnih) meseci.

Primer 2 (atipičan slučaj): Nađi Greogorijanski datum Kineske Nove godine 1985 n.e. Zimski solsticij i mlad Mesec se pojavljuju 22. decembra 1984.

Prva teškoća je da mesec 11 ima oba glavna člana 11 i 12. Takođe ćemo videti da mesec koji počinje 20. februara ne može biti interkalarni. Ovo se otkriva nalaženjem sledećeg solsticija, koji se mora pojaviti u 11. mesecu i proverom broja mladih meseca. 1985, P-11 se pojavljuje 22 decembra, a mlad Mesec koji počinje u 11. mesecu se pojavljuje 12. decembra. Idući unatrag, u 1985. nalazimo mlade Mesece 13. novembra, 14. oktobra, 15. septembra, 16. avgusta, 18. jula, 18. juna, 20. maja, 20. aprila, 21. marta, 20. februara i 21. januara. Pošto ima samo dvanaest mladih meseca od 11. meseca 1984. do 11. meseca 1985., nema mesta za interkalarni mesec. Tako da je pravilna sekvenca meseci sledeća:

Kineska Nova godina, prema tome, pada na 20. februar 1985.

Uopšte, prvi korak pri proračunu Kineskog kalendara je da se proveri postojanje godine sa umetanjem. Ovo se može uraditi određivanjem datuma zimskog solsticija i 11. meseca pre ili perioda za koji smo zainteresovani, i zatim brojanjem interventnih mladih meseca.

Često se publikovane tabele kineskih kalendara ne slažu sa stvarnim kineskim kalendarom. Neke tabele su zasnovane na srednjim, ili uprošćenim, kretanjima Sunca i Meseca. Neke su proračunate za druge meridijane, a ne za 120° istočno. Neke sadrže pravilo da jedanaesti, dvanaesti i prvi mesec nisu nikad praćeni umetnutim mesecom. Ovo nekad nije navedeno kao pravilo, već je posledica brze promene sunčeve longitude kada je Zemlja blizu perihela. Ovakav iskaz je neispravan kada se kretanja Sunca i Meseca tačno računaju.

14 ALGORITMI ZA KONVERZIJU KALENDARA

Nadamo se da se kroz ceo tekst uočava tendencija da se Julijanski dani koriste kao najbolja osnova za raznoliku stručnu i naučnu praksu. Posebno se može naglasiti njihova skoro nezaobilazna uloga u lakom i brzom konvertovanju datuma jednog kalendara u datume drugog kalendara i slično.

Dakle, julijanski dan je najbolji oslonac konverzije iz kalendara u kalendar, ukoliko su ovi poslednji zasnovani na fiksnim pravilima. Postoje raličiti postupci za prelaz sa jednog kalendarskog sistema na drugi - za konvwerziju kalendara. Ovde ćemo dati nekoliko algoritama koji su mahom zasnovani na radovima Harvey-a, Hatcher-a, Parisot-a, Fliegel-a i Van Flandren-a.

U ovim algoritmima isključivo je upotrebljena aritmetika celih brojeva, tj., svi ostaci deljenja su odbačeni.

Julijanski dani se računaju od podneva do podneva. Prema tome, izračunati Julijanski dan se odnosi na podne tekućeg kalendarskog datuma. Oznake su

Jd = Julijanski dan
G = kalendarska godina
M = mesec
D dan u mesecu

Sve promenljive su celi brojevi.

14.1 Određivanje dana u nedelji

14.2 Pretvaranje Gregorijanskih kalendarskih datuma u Julijanske dane

14.3 Pretvaranje islamskih tabličnih kalendarskih datuma u julijanske dane

14.4 Pretvaranje Indijskog građanskog kalendara u Julijanske dane

14.5 Pretvaranje Julijanskog kalendarskog datuma u Julijanske dane

12.10 REFERENCE

PRILOG I

PRILOG II